銀行からの借入金の利息や返済額をエクセルでかんたんに計算

※記事内に広告を含む場合があります

銀行や信用金庫から資金調達をする場合、事前に事業計画の提出を求められることがあります。

売上や利益については事業主の思惑が入りますが、借入金の返済計画も含めて事業計画を練らなくてはなりません。

しかし、借入金の利息や返済額の計算はとにかくややこしく、銀行からもらう「返済予定表」を頼りにしている方も多いと思います。

借入金の利息計算は電卓を使うと面倒なのですが、エクセルを使うと簡単に結果を算出できます。

もちろん、普段エクセルを使い慣れていない人でもこれから解説する通りに実践すれば、かんたんに将来の返済計画が立てられ、資金繰りの改善や事業計画の作成に役立てることができます。

今回は、借入金の利息や返済総額を計算する４つの方法を、エクセルを使って誰でも使えるように解説します。

元金均等返済と元利均等返済

借金の返し方には「元金均等返済」と「元利金等返済」の２種類がありますが、私の経験上「元金均等返済」が選択されることが多いように思います。

返済方法によって毎月のキャッシュフローや返済総額が変わってくるので、どちらを選択しているか確認することをおすすめします。

毎月のキャッシュフローを安定させたい場合は「元利均等方式」を選択（ただし返済総額は多くなる）し、返済総額（利息）を少なくしたい場合は「元金均等方式」を選択（ただし最初の頃は返済額が増える）します。

日割り計算が基本

銀行や信用金庫からの借入は、基本的に「日割り計算」で行われます。

また、借入の契約をした場合は、返済開始日を１～２ヶ月遅らせ、その間は利息だけを支払うという形式を取ることも少なくありません。

これらの仕組みに柔軟に対応できる日割り計算の方法がこちらです。

借入利率が年３％なら「３％ ÷ 365日」をして利率を１日単位にします。その後、１ヶ月の借入日数（多くの場合30日または31日）を掛け、これを借入残高に掛けることで利息計算ができます。

元金均等方式の場合は、「毎月の返済元金＋利息」が返済額となります。元利均等方式なら月々の返済額は固定です。

PMT関数で毎月の支払額を計算する

返済方式が「元利均等返済」の場合、エクセルのPMT関数を使うことで毎月の支払額を計算できます。

利率

借入金利のことです。利率は12ヶ月で割り算して使います

期間

返済回数のことです。１年だったら12回、10年なら120回です

現在価値

現在の借入金残高を入力します

将来価値（省略可能）

最後に残る金額を入力しますが、多くの場合最後は０円になりますので、省略可能です

支払期日（省略可能）

０を入力すると月末、１を入力すると月初で計算しますが、省略可能です

PMT関数は、元利均等返済のケースを想定しているので、毎月の返済額は同じです。

「この金利で24回払いだったら毎月の返済額はいくらになるのだろうか…」という疑問に対する答えを知りたい時に使えます。

まず最初に、エクセルに必要な数値を入力します。
今回は、金利2.5％、期間は60回（５年）、借入残高500万円としました。金利の部分に「％」という単位を入れるのを忘れないでください。

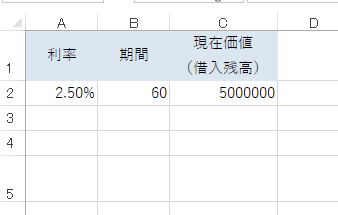
エクセルの画面上部にある「数式」タブを選択すると、一番左に「関数の挿入」というボタンが表示されます。計算結果を表示させたい位置（今回はD2セル）にカーソルを置いて「関数の挿入」ボタンを押します。

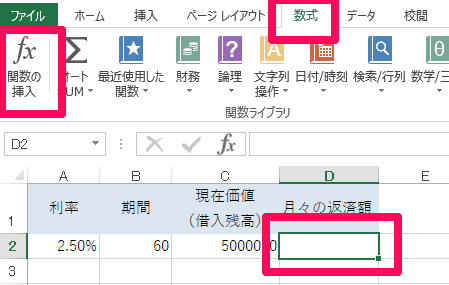
「関数の挿入」を押すとダイアログが立ち上がります。関数名がたくさん並んでいるリストの中から「PMT」を選択し、「OK」をクリック。

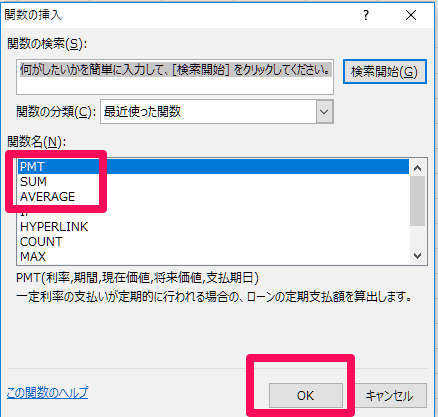
「関数の引数」の入力画面です。画像の通り、セル番号をベタ打ちしても良いのですが、「利率にカーソルを合わせる　→　A2セルを選択　→　期間にカーソルを合わせる　→　B2セルを選択…」とマウスでクリックしていくだけで、自動的にセル番号が入力されます。

ただし、利率の部分だけは「/12」を入れることを忘れないよう注意してください。「A2/12」は「A2 ÷ 12」を意味します。（金利を12ヶ月で割り算するため）

PMT関数では「将来価値」と「支払期日」は省略できるので、今回は空白にしておきます。入力が完了したら「OK」をクリックします。

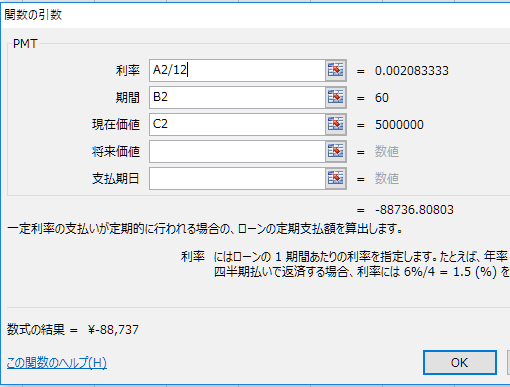
すると、月々の返済額（D2セル）に計算結果が表示されます。金利2.5％、期間60回（５年）、借入残高500万円の場合、毎月88,737円の返済が必要だとわかりました。

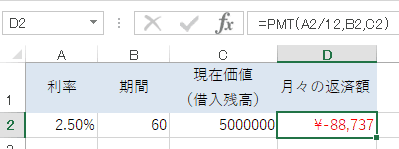
ちなみに、元利均等返済は毎月の返済額が固定されているので、「月々の返済額88,737円 × 60回 ＝ 5,324,220円」が返済総額となります。

利率、期間、現在価値（借入残高）の部分は「変数」になっているので、自由に変更可能です。

例えば、借入金額を600万円にしたら月々の返済額はどれくらい増えるのだろう、期間を60回（５年）から84回（７年）に伸ばすと毎月の返済額はどれくらい減るのだろうといった「感応度分析」ができ、事業計画の策定に活かせます。

PPMT関数で元金部分だけを計算

前述のPMT関数を使うと、元利均等方式を選択した場合の毎月の返済額（元金＋利息の合計）を知ることができました。

しかし、毎月の返済額の内訳（元金がいくらで利息がいくらなのか？）についてはPMT関数では計算できません。

元利均等方式で「元金部分」だけを知るには「PPMT関数」を使います。

利率

借入金利のことです。利率は12ヶ月で割り算して使います

期

何回目の返済を計算するか

期間

返済回数のことです。１年だったら12回、10年だったら120回です

現在価値

現在の借入金残高を入力します

将来価値（省略可能）

最後に残る金額を入力しますが、多くの場合最後は０円になりますので、省略可能です

支払期日（省略可能）

０を入力すると月末、１を入力すると月初で計算しますが、省略可能です

具体的な計算方法は先ほどとほとんど同じです。

PPMT関数では「期（何回目の返済か？）」を指定する必要があるため、新しく「期」という項目を追加しました。

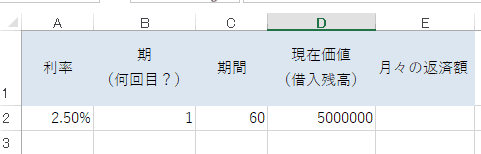
カーソルを「月々の返済額（E2セル）」に合わせ、エクセルの上部の「数式」タブを選びます。一番左の「関数の挿入」をクリックします。

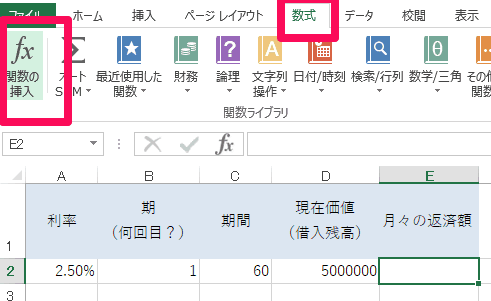
ダイアログが立ち上がりますので、「関数の挿入」で「PPMT」を選択します。候補に表示されていない場合は、「関数の検索」で「PPMT」と入力すれば見つかるはずです。

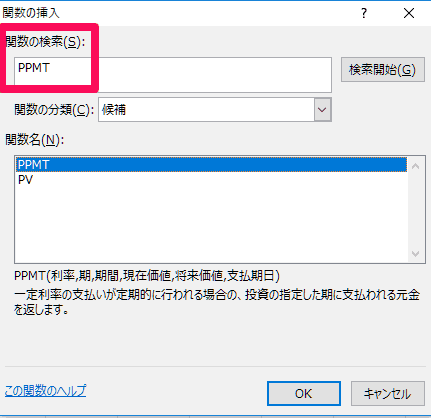
「関数の引数」を設定します。利率の部分には「/12」を入れることを忘れないように注意します。

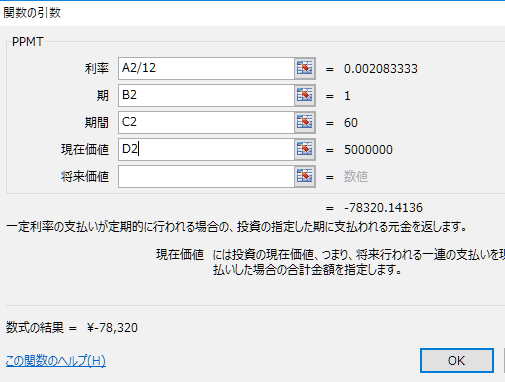
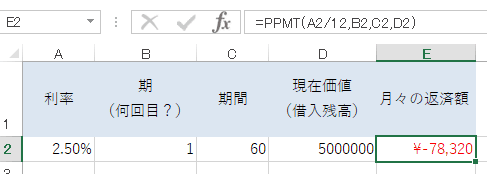
E2セルに計算結果が表示されます。利率2.5％、期間60回（５年）、借入金額500万円の場合、１回目の返済金額の元金は78,320円であることがわかりました。

IPMT関数で利息部分だけを計算

PPMT関数は、元利均等方式の「元金」部分を計算する関数でしたが、同じく「利息」部分を計算する関数に「IPMT関数」があります。

使い方はPPMT関数と全く同じです。先ほどの計算結果を表示した「E2セル」の「PPMT」を「IPMT」と書き換えるだけで、利息がいくらか算出できます。

元金均等方式を計算するISPMT関数

私の経験上、銀行からの借入では「元金均等返済」が多く使われているように思います。

元利均等返済は毎月の「元金＋利息」の返済額が固定でしたが、元金均等方式は元金部分が固定となっているのが特徴です。

つまり、当初の返済額は増えますが、返済回数をこなしていくに従い、月々の返済額が減っていくのが特徴です。

元金均等方式の「利息部分」を計算するエクセル関数に「ISPMT関数」があります。

利率

借入金利のことです。利率は12ヶ月で割り算して使います

期

何回目の返済を計算するか（１回目の返済は０、２回目の返済は１を入力）

期間

返済回数のことです。１年だったら12回、10年なら120回です

現在価値

現在の借入金残高を入力します

使い方は前述した「IPMT関数」とほぼ同じです。

カーソルを「月々の返済額（E2セル）」に合わせ、エクセルの上部の「数式」タブを選びます。一番左の「関数の挿入」をクリックします。

ダイアログ「関数の挿入」で「ISPMT」を選択します。候補に表示されていない場合は、「関数の検索」で「ISPMT」と入力します。

「関数の引数」を設定します。利率の部分には「/12」を入れることを忘れないように注意します。

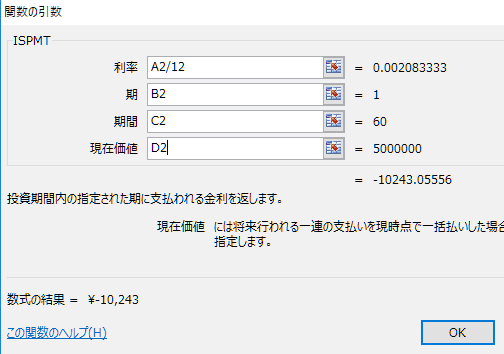
E2セルに計算結果が表示されます。利率2.5％、期間60回（５年）、借入金額500万円の場合、１回目２回目の返済金額の利息は10,243円であることがわかりました。（上述した誤表記の修正に伴い、下記の計算結果は２回目の返済額となります）

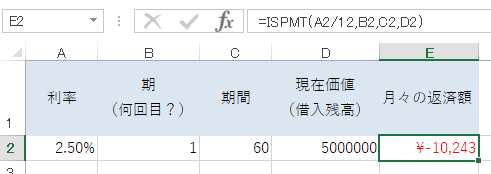
元金均等方式の元金を計算

元金均等方式はその名の通り、元金部分は固定です。

500万円を60回（５年）で返済する場合は単純に「500万円 ÷ 60回 ＝ 83,333円」が月々の返済元金となります。

つまり、ISPMT関数で算出した「利息部分」＋「固定されている元金部分」の合計が、毎月の返済額となります。

元金均等方式の場合、初回の返済額が最も大きく、その後返済額は減っていきます。

ローン返済シミュレーターを作りました

これまで、エクセルで借入金の返済額を計算する方法を説明してきました。

より簡単にローン返済の計算ができる方法はないかと考え、当サイト「今日の経営」が独自に作成したローン返済シミュレーターをご案内します。

返済額シミュレーターの特長は以下の通りです。

• ブラウザに hensai.app と入力するだけでアクセスできる
• 元金均等返済・元利均等返済の選択が可能
• 最長10年間で１ヶ月ごとの借入期間を指定できる
• シミュレーション結果をグラフで表示
• 月々の返済予定表を表示

ぜひ、ブックマークの上ご活用ください。

今日の経営 ローン返済シミュレーターはこちら

データテーブルを使った感応度分析

エクセルには「データテーブル」という強力な機能が付いています。

データテーブルを活用することで、感応度分析（シミュレーション）ができます。

やや上級編となりますが、先ほどのPMT関数（元利均等方式の月々の返済額（元金＋利息）を計算）を用いてデータテーブルの使い方を解説します。

先ほどと同じく、基本となる数値を、金利2.5％、期間は60回（５年）、借入残高500万円とします。

こちらがPMT関数の計算結果です。上記の条件で元利均等方式を選択した場合、毎月の返済額は88,737円になることがわかりました。

このように基本となる計画を作った後に、

• 借入利率が変化した場合はどうなるか？
• 返済期間５年で可能な限り借入額を増やすにはどうすればよいか？

といった様々なシミュレーションが作れると、より事業計画を具体的に検討できます。

今回は「月々の返済額を10万円以内に抑える」という条件を置いた上で、借入金額を最大化するシミュレーションを行います。

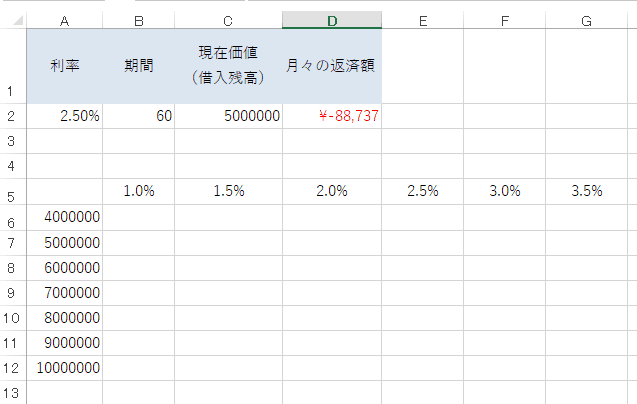
まずはじめに、利率と借入額の予測を作成します。
列の部分に想定借入額として400万円～1,000万円までを入力、行の部分に想定借入利率として1.0％～3.5％を入力しました。

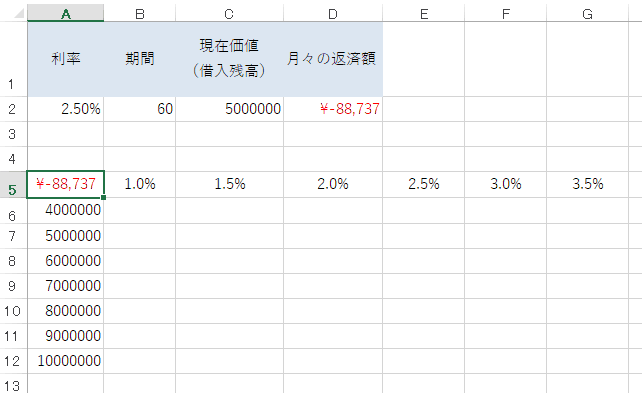
次に、想定借入額と想定借入利率のクロスする部分（A5セル）に「=D2」と入力し、D2セルで算出したPMT関数の計算結果（月々の返済額）を表示させます。

先ほど想定数値を入力したエリアをマウスで選択して囲います。その後、エクセル上部の「データ」タブを選び、「What-IF分析」から「データテーブル」を選択します。

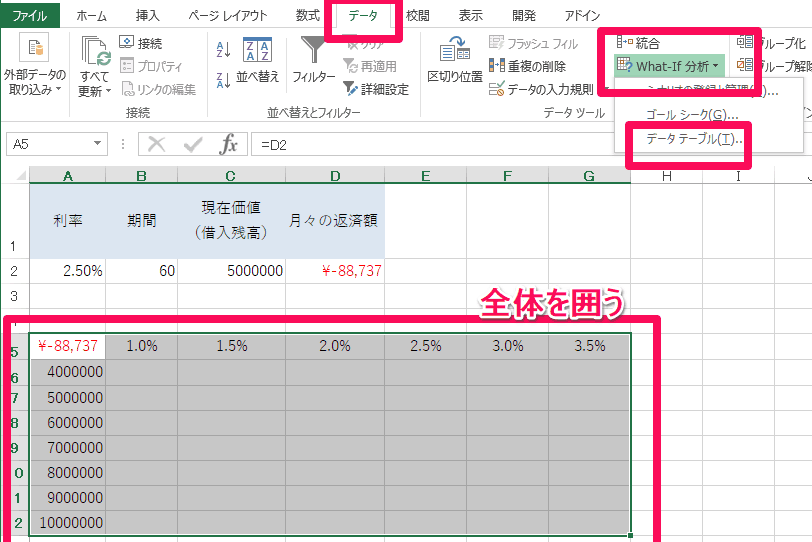
ダイアログが立ち上がるので「行の代入セル」にカーソルを合わせて「A2セル」をクリック、「列の代入セル」にカーソルを合わせて「C2セル」をクリックします。

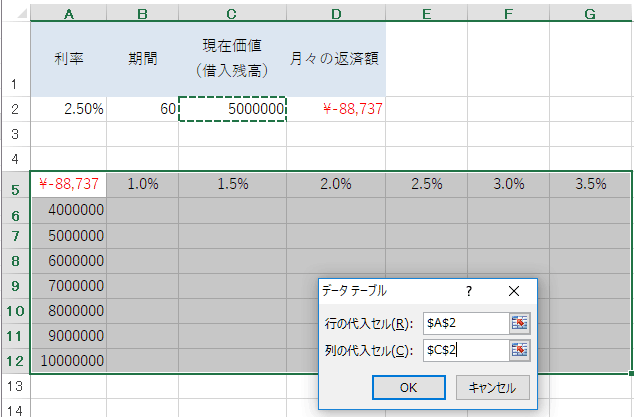
すると、行・列で想定していた数値のあらゆる組み合わせで、月々の返済額がいくらになるかをエクセルが自動計算してくれます。

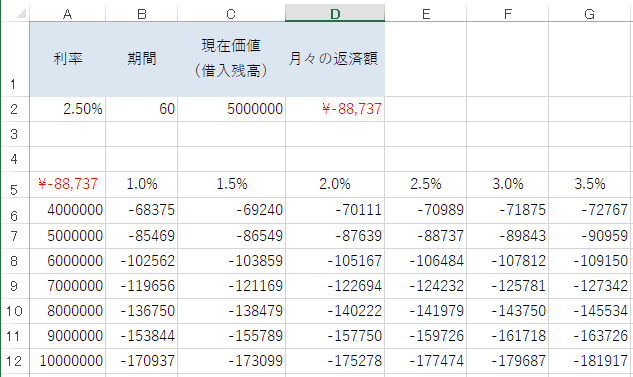
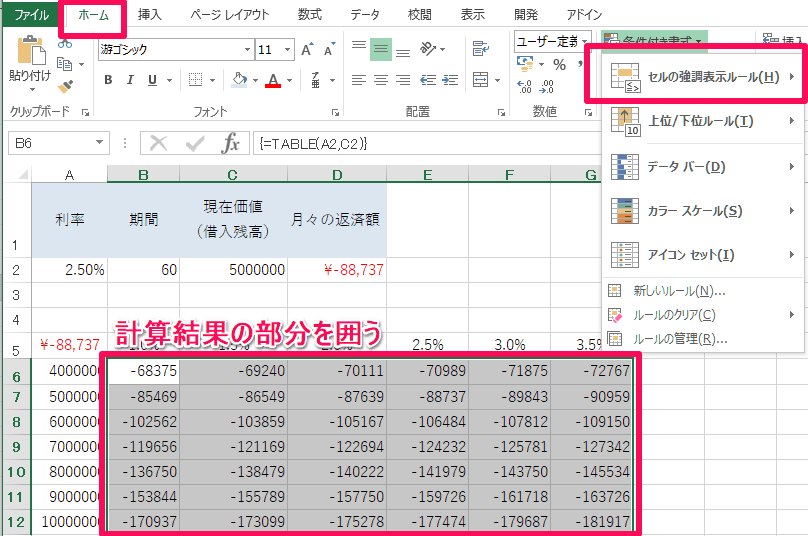
これだと少し見にくいので、計算結果の表示部分を選択し「ホーム」タブにある「条件付き書式」から、「セルの強調表示ルール」を選びます。セルの強調表示ルールは「指定の値より大きい」を選択します。

今回は「月々の返済額を10万円以内に抑える」ことが条件でしたので、「-100000」と入力して「OK」をクリック。

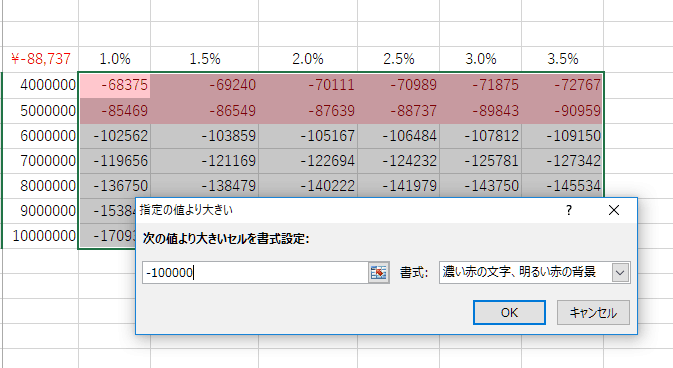
すると、データテーブルのシミュレーションの中から、月々の返済額が10万円以内の枠だけが強調表示され見やすくなります。

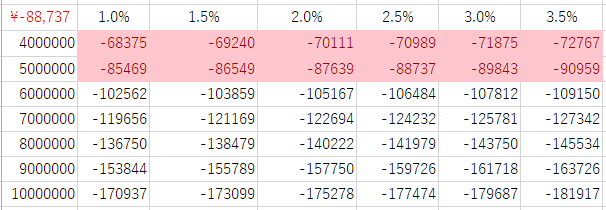
今回の計算結果では、借入金額を600万円にしてしまうと、仮に借入利率を1.0％まで引き下げても月々の返済額が10万円を超えてしまうことがわかりました。

月々の返済額を10万円以下にするという資金繰りで事業計画を作る場合、返済期間が５年（60回返済）なら500万円が借入の限界のようです。

逆に、当初予想していた2.5％の金利で審査が通らなくても、金利を引き上げることで、他の金融機関が融資の審査を通してくれるかもしれません。

今回のシミュレーションでは、借入金額が500万円なら、金利が3.5％まで上がっても月々の返済額は10万円以下となり、計画通りに事業を進めることが可能だとわかります。

信用保証料に気をつける

最後に、信用保証料について触れておきます。

銀行や信用金庫から融資を受ける場合、金融機関がリスクを負って貸し出す「プロパー融資」と、信用保証協会を通す「信用保証協会付き融資」があります。

創業当初の企業などは大抵、プロパー融資は受けられず、まずは保証協会付き融資になるケースが多いです。

しかし、信用保証協会を通す場合は別途「信用保証料」を負担する必要があります。

信用保証料は融資の契約を結ぶ時に払い込むことが多いのですが、これは実際の借入金利には含まれていません。

つまり、年1.2％の利率で借りられると思っていても、信用保証料が0.8％の利息相当額になっている場合は、実質的な借入利率は2.0％として考える必要があります。

低金利だと思って借りたは良いものの、実際の支払額は「利息＋信用保証料」となっており、金利換算すると実は高利で借りていたということにならないよう注意が必要です。

信用保証協会付きの融資を受ける場合は、金融機関の担当者に「信用保証料を含んだ実質金利を教えて欲しい」と言えば、計算してくれます。

ちなみに、日本政策金融公庫についてはすべてプロパー融資ですので、信用保証料などが加算されることはありません。

続いての記事は「開業まもない事業者が資金調達先として検討できる５つの窓口」です。創業期の資金調達先をまとめています。